Това е задача номер 24 от матурата по математика за седми клас от 22.05.2017 г.
Според родители и ученици обаче в условието на задачата има некоректност, която е подвела много от седмокласниците, а именно, че триъгълникът с тези параметри е тъпоъгълен, а не остроъгълен, както е уточнено в условието на задачата. Грешното условие би довело до некоректни чертежи и блокаж у децата.
Ето коментара на една майка:
Ще се окаже, че е тъпоъгълен. Предупреждавам, че материалът надолу не е за 7 клас.
Косинусова теорема за триъгълника ни дава: AC^2=AB^2+BC^2 -2.AB.BC.cos30 AC^2= 196 +144-2.14.12.0,866 AC^2=49,0155
И сега с проверка се вижда, че AB^2>BC^2+AC^2 196>49,0155+144 newsm78 196>193,0155 => тъпоъгълен
НАЧЕРТАНО И С AutoCAD (за проверка). Единият ъгъл е 91 градуса. Тоест с тези данни задачата не отговаря на първоначалното условие!
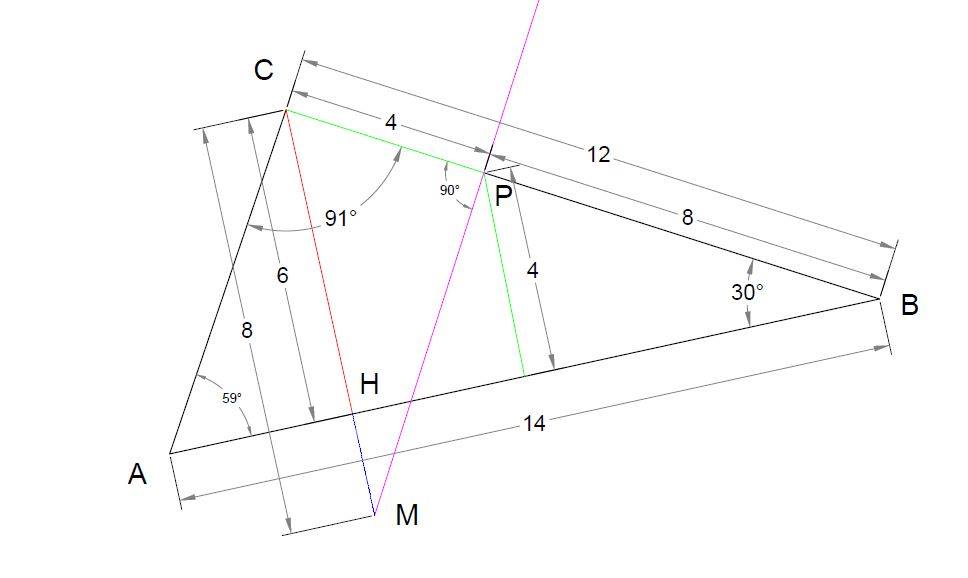
Какво ще кажете, математици? Грешно ли е зададена задача 24?
Свързани статии (по етикет)
- Най-популярни
- Най-нови
Тагове
Вижте тази публикация в Instagram.World is such a lovely playpen! #babybobby
Публикация, споделена от Maria Peeva (@mimipeeva) на